So far, in this week of khmer blog posts (1, 2, 3), we've been focusing on the read-to-graph aligner ("graphalign"), which enables sequence alignments to a De Bruijn graph. One persistent challenge with this functionality as introduced is that our De Bruijn graphs nodes are anonymous, so we have no way of knowing the sources of the graph sequences to which we're aligning.
Without being able to label the graph with source sequences and coordinates, we can't do some pretty basic things, like traditional read mapping, counting, and variant calling. It would be nice to be able to implement those in a graph-aware manner, we think.
To frame the problem, graphalign lets us query into graphs in a flexible way, but we haven't introduced any way to link the matches back to source sequences. There are several things we could do -- one basic idea is to annotate each node in the graph -- but what we really want is a lightweight way to build a labeled graph (aka "colored graph" in Iqbal parlance).
This is where some nice existing khmer technology comes into play.
Partitioning, tagging, and labelhash
Back in 2012, we published a paper (Pell et al., 2012) that introduced a lightweight representation of implicit De Bruijn graphs. Our main purpose for this representation was something called "partitioning", in which we identified components (disconnected subgraphs) of metagenome assembly graphs for the purpose of scaling metagenome assembly.
A much underappreciated part of the paper is buried in the Materials,
For discovering large components we tag the graph at a minimum density by using the underlying reads as a guide. We then exhaustively explore the graph around these tags in order to connect tagged k-mers based on graph connectivity. The underlying reads in each component can then be separated based on their partition.
The background is that we were dealing with extremely large graphs (30-150 billion nodes), and we needed to exhaustively explore the graphs in order to determine if any given node was transitively connected to any other node; from this, we could determine which nodes belonged to which components. We didn't want to label all the nodes in the graph, or traverse from all the nodes, because this was prohibitive computationally.
A sparse graph covering
To solve this problem, we built what I call a sparse graph covering, in which we chose a subset of graph nodes called "tags" such that every node in the graph was within a distance 'd' of a tag. We then used this subset of tags as a proxy for the graph structure overall, and could do things like build "partitions" of tags representing disconnected components. We could guarantee the distance 'd' by using the reads themselves as guides into the graph (Yes, this was one of the trickiest bits of the paper. ;)
Only later did I realize that this tagging was analogous to sparse graph representations like succinct De Bruijn graphs, but that's another story.
The long and short of it is this: we have a nice, simple, robust, and somewhat lightweight way to label graph paths. We also have functionality already built in to exhaustively explore the graph around any node and collect all tagged nodes within a given distance.
What was missing was a way to label these nodes efficiently and effectively, with multiple labels.
Generic labeling
Soon after Camille Scott, a CS graduate student at MSU (and now at Davis), joined the lab, she proposed an expansion to the tagging code to enable arbitrary labels on the tags. She implemented this within khmer, and built out a nice Python API called "labelhash".
With labelhash, we can do things like this:
lh = khmer.CountingLabelHash(...) lh.consume_fasta_and_tag_with_labels(sequence_file)
and then query labelhash with specific sequences:
labels = lh.sweep_label_neighborhood(query, dist)
where 'labels' now contains the labels of all tags that overlap with 'query', including tags that are within an optional distance 'dist' of any node in query.
Inconveniently, however, this kind of query was only useful when what you were looking for was in the graph already; it was a way to build an index of sequences, but fuzzy matching wasn't possible. With the high error rate of sequencing and high polymorphism rates in things we worked on, we were worried about its poor effectiveness.
Querying via graphalign, retrieving with labelhash
This is where graphalign comes in - we can query into the graph in approximate ways, and retrieve a path that's actually in the graph from the query. This is essentially like doing a BLASTN query into the graph. And, combined with labelhash, we can retrieve the reference sequence(s) that match to the query.
This is roughly what it looks like, once you've built a labelhash as above. First, run the query:
aligner = khmer.ReadAligner(lh.graph, trusted_coverage, 1.0) score, graph_path, query_path, is_truncated = aligner.align(query)
and then retrieve the associated labels:
labels = lh.sweep_label_neighborhood(graph_path)
...which you can then use with a preexisting database of the sequence.
Why would you do any of this?
If this seems like an overly complicated way of doing a BLAST, here are some things to consider:
- when looking at sequence collections that share lots of sequence this is an example of "compressive computing", in which the query is against a compressed representation of the database. In particular, this type of solution might be good when we have many, many closely related genomes and we want to figure out which of them have a specific variant.
- graphs are notoriously heavyweight in general, but these graphs are actually quite low memory.
- you can do full BLASTX or protein HMM queries against these graphs as well. While we haven't implemented that in khmer, both a BLAST analog and a HMMER analog have been implemented on De Bruijn graphs.
- another specific use case is retrieving all of the reads that map to a particular region of an assembly graph; this is something we were very interested in back when we were trying to figure out why large portions of our metagenomes were high coverage but not assembling.
One use case that is not well supported by this scheme is labeling all reads - the current label storage scheme is too heavyweight to readily allow for millions of labels, although it's something we've been thinking about.
Some examples
We've implemented a simple (and, err, somewhat hacky) version of this in make-index.py and do-align.py.
To see them in action, you'll need the 2015-wok branch of khmer, and a copy of the prototype (https://github.com/dib-lab/2015-khmer-wok4-multimap) -- see the README for full install instructions.
Then, type:
make fake
and you should see something like this (output elided):
./do-align.py genomes reads-a.fa read0f 1 genomeA read1f 1 genomeA read2f 1 genomeA ./do-align.py genomes reads-b.fa read0f 1 genomeB read1f 1 genomeB read2r 1 genomeB
showing that we can correctly assign reads sampled from randomly constructed genomes - a good test case :).
Assigning reads to reference genomes
We can also index a bunch of bacterial genomes and map against all of them simultaneously -- target 'ecoli' will map reads from E. coli P12B against all Escherichia genomes in NCBI. (Spoiler alert: all of the E. coli strains are very closely related, so the reads map to many references!)
Mapping reads to transcripts
It turns out to be remarkably easy to implement a counting-via-mapping approach -- see do-counting.py. To run this on the same RNAseq data set as in the counting blog post, run build the 'rseq.labelcount' target.
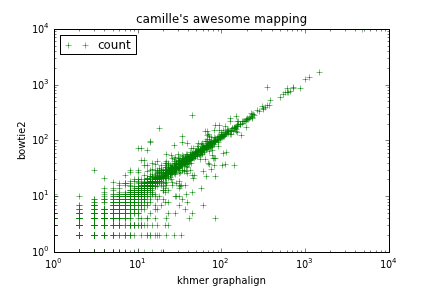
Figure 1: Mapping counts via graphalign/labelhash (x axis) vs bowtie2 (y axis).
Flaws in our current implementation
A few points --
- we haven't introduced any positional labeling in the above labels, so all we can do is retrieve the entire sequence around submatches. This is enough to do some things (like counting transcripts) but for many purposes (like pileups / variant calling via mapping) we would need to do something with higher resolution.
- there's no reason we couldn't come up with different tagging and labeling schemes that focus on features of interests - specific variants, or branch points for isoforms, or what have you. Much of this is straightforward and can be done via the Python layer, too.
- "labeled De Bruijn graphs" are equivalent in concept to "colored De Bruijn graphs", but we worry that "colored" is already a well-used term in graph theory and we are hoping that we can drop "colored" in favor of "labeled".
Appendix: Running this code
The computational results in this blog post are Rather Reproducible (TM). Please see https://github.com/dib-lab/2015-khmer-wok4-labelhash/blob/master/README.rst for instructions on replicating the results on a virtual machine or using a Docker container.
Comments !